限幅滤波法

又称程序判断滤波法

优点

能够有效克服因偶然因素引起的误差

缺点

周期性差、无法抑制周期性误差

过程简述

根据经验得出两次采样允许的最大误差值(记为A)
每次采样得到新值时做出如下判断:
- 如果本次值与上次值之差<=A 那么本次值有效
- 反之，本次值无效

算法实现

#define A 10  // 最大误差值
char value; // 上一次采样值
char filter()
{
    char new_value; //本次采样值
    new_value = get_ad();
   if ( ( new_value - value > A ) || ( value - new_value > A )
      return value;
   return new_value;
}

中位值滤波法

优点

能有效克服因偶然因素引起的波动干扰
对温度、液位等变化缓慢的被测参数具有良好的滤波效果

缺点

不适合对流量、速度等快速变化参数进行操作

过程简述

连续采样N次(N取奇数)
把N次采样值按照大小排列
取数据序列中的中位数为本次采样的有效值

算法实现

#define N 11 // 连续采样次数(取奇数)
char filter()
{
    char value_buf[N];
    char count, i, j, temp;
    // 进行采样
    for (count = 0; count < N; count++)
    {
        value_buf[count] = get_ad();
        delay();
    }
    // 排序
    for (j = 0; j < N - 1; j++)
    {
        for (i = 0; i < N - 1 - j; i++)
        {
            if (value_buf[i] > value_buf[i + 1])
            {
                temp = value_buf[i];
                value_buf[i] = value_buf[i + 1];
                value_buf[i + 1] = temp;
            }
        }
    }
    return value_buf[(N - 1) / 2]; //取中位数
}

算术平均滤波法

优点

适用于对一般随机干扰的信号进行滤波
由于平均值的存在，信号在某一数值范围附近上下波动

缺点

对于测量速度较慢或要求数据计算速度较快的实时控制不适用
比较浪费RAM空间

过程简述

计算公式如下:
$$\overline y = \frac{1}{N}\sum\limits_{i = 1}^N {{Y_i}}$$

连续取N个采样值进行算术平均运算
N值较大时: 信号平滑度较高，但灵敏度较低
N值较低时: 信号平滑度较低，但灵敏度较高
N值的选取: 一般来讲，流量N=12 , 压力N=4
N可以取2的整数幂，以便通过移位快速进行除法运算

算法实现

#define N 12 // 采样次数
char filter()
{
    int sum = 0;
    // 完成相应次数的数据采样
    for (count = 0; count < N; count++)
    {
        sum + = get_ad();
        delay();
    }
    return (char)(sum >> N);
}

中位值平均滤波法

又称防脉冲干扰平均滤波法，实际上相当于"中位值滤波法" + "平均值滤波法"

优点

融合了两种算法的优点
对于偶然出现的脉冲性干扰，可消除由于脉冲干扰引起的采样值偏差

缺点

与平均值滤波法一样，测量速度较慢
比较浪费RAM

过程简述

连续采样N个数据，去掉一个最高值和一个最低值
计算N-2个数据的平均值

算法实现

#define N 12 // 采样次数
char filter()
{
    char count, i, j;
    char value_buf[N];
    int sum = 0;
    /* 连续进行相应的次数的采样 */
    for (count = 0; count < N; count++)
    {
        value_buf[count] = get_ad();
        delay();
    }
    /* 对数组缓存区进行排列 */
    for (j = 0; j < N - 1; j++)
    {
        for (i = 0; i < N - 1 - j; i++)
        {
            if (value_buf[i] > value_buf[i + 1])
            {
                temp = value_buf[i];
                value_buf[i] = value_buf[i + 1];
                value_buf[i + 1] = temp;
            }
        }
    }
    /* 不考虑最小值和最大值 */
    for (count = 1; count < N - 1; count++)
        sum += value[count];
    return (char)(sum / (N - 2));
}

加权平均值滤波算法

优点

对算数平均值中的信号平滑度和灵敏度进行协调

缺点

对于传递滞后时间较小、采样周期较长、变化较为缓慢的信号处理效果较差

过程简述

计算公式如下:
$${y_n} = \frac{1}{N}\sum\limits_{i = 1}^{N - 1} {{C_i}} {X_{n - i}}$$

连续进行N次采样
对每次采样的结果乘以加权系数,计算出每次结果的总和sum
sum / N 即为结果

几个注意点

加权系数均小于1，且它们的总和为1
加权系数一般先小后大，即越接近现在时刻的权重越大，以此来反映实际的值
在实际操作中需要调整好加权系数

算法实现

#define N 12 // 采样次数
float weightedAverage[N] = {...} //加权系数
char filter()
{
    int sum = 0;
    // 完成相应次数的数据采样
    for (count = 0; count < N; count++)
    {
        sum + = get_ad() * weightedAverage[N];
        delay();
    }
    return (char)(sum / N);
}

另一种实现

#define N 11 // 连续采样次数
char filter(int bufLength, int *pArray) // 这里，可以让bufLength = N pArray指向存储值的数组
{
    int i = 0;
    int data = 0;
    int num = 0;
    for (i = 0; i < bufLength; i++)
    {
        num += (*(pArray + i) * i); //计算加权和

        data += i; //计算权值
    }

    return num / data; //返回加权平均值
}

递推平均滤波法

又称滑动平均滤波法

优点

对周期性干扰有良好的抑制作用，平滑度高
适用于高频振荡的系统，对处理数据波动较大的采样值具有较为良好的滤波效果

缺点

灵敏度低
对偶然出现的脉冲性干扰的抑制作用较差
不易消除由于脉冲干扰所引起的采样值偏差
不适用于脉冲干扰比较严重的场合
比较浪费RAM

过程简述

把连续N个采样值看成一个队列(队列长度即为N)
将每次采样到的一个新数据放到队尾，若此时队列已满，丢弃队首原有的数据，这样在队列中始终保持有N个有效数据(满足先进先出原则)
计算队列中数据的平均值作为滤波结果
关于N值的选取: 流量N=12 压力N=4 液面N=4~12 温度N=1~4

算法实现

#define N 12       // 采样次数(队列长度)
char value_buf[N]; // 用数组实现简单的队列
char i = 0;
char filter()
{
    char count;
    int sum = 0;
    value_buf[i++] = get_ad();
    if (i == N)
        i = 0; //队列满，覆盖队列头部的数据
    for (count = 0; count < N, count++)
        sum = value_buf[count];
    return (char)(sum / N); // 取平均值
    }

加权递推平均滤波法

是对递推平均滤波法的改进，即不同时刻的数据加以不同的权。具体和加权平均平均值滤波的注意事项差不多。

优点

适用于有较大纯滞后时间常数的对象和采样周期较短的系统

缺点

-对于传递滞后时间常数较小，采样周期较长，变化缓慢的信号，不能够迅速反映系统当前所受干扰的严重程度，滤波效果较差。

过程简述

和递推平均滤波算法类似，在每次取得的采样结果乘以相应的权值后计算得出平均值

算法实现

#define N 12       // 采样次数(队列长度)
char value_buf[N]; // 用数组实现简单的队列
char code coe[N] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}; // 加权系数表
char code sum_coe = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12; // 总数
char i = 0;
char filter()
{
    char count;
    int sum = 0;
    value_buf[i++] = get_ad();
    if (i == N)
        i = 0; //队列满，覆盖队列头部的数据
    for (count = 0; count < N, count++)
        sum += value_buf[count] * coe[count]; // 取得加权后的总和
    return (char)(sum / sum_coe); 
}

低通滤波算法

一阶滞后滤波法

优点

对于周期性干扰具有良好的抑制作用
适用于波动频率较高的场合

缺点

相位滞后，灵敏度低'
滞后程度取决于系数a的大小
不能消除滤波频率高于采样频率的1/2的干扰信号

过程简述

计算公式如下：
$${{\rm{y}}_n} = (1 - a){x_n} + a*{y_{n - 1}}$$
其中,Xn为本次采样结果,Yn-1为上次滤波结果

算法实现

#define a 0.01 // 滤波系数a（0-1）
char filter(void)
{
    char new_value; // 本次采样值
    static latest_value = 0; //最后一次的滤波值
    new_value = get_ad();
    latest_value = a * latest_value + (1.0f - a) * new_value;
    return latest_value;
}

消抖滤波法

优点

对于变化缓慢的被测参数有较好的滤波效果
可避免在临界值附近控制器的反复开/关跳动或显示器上数值抖动

缺点

不适用于快速变化的参数
如果在计数器溢出时采样到的恰好是干扰值，则将会将干扰值当作有效值进行处理导入到系统中

过程简述

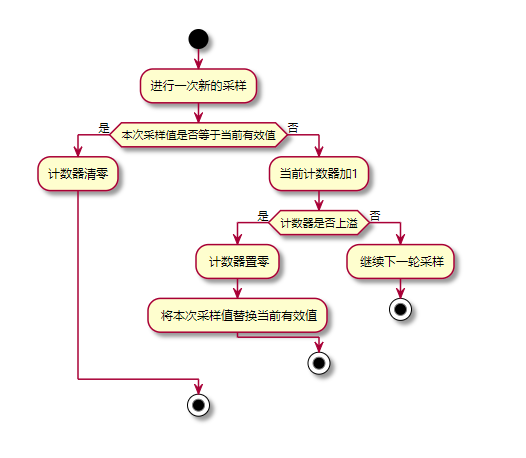
算法实现

#define N 12 // 采样次数上限
char filter()
{
    char count = 0;
    char new_value; //
    new_value = get_ad();
    while (value != new_value)
    {
        count++;
        if (count >= N)
            return new_value;
        delay();
        value = get_ad();
    }
    return value;
}

最后编辑时间为: March 27th , 2019 at 10:20 pm
本文由 air 创作，采用知识共享署名 4.0 国际许可协议进行许可
可自由转载、引用，但需署名作者且注明文章出处

各种滤波算法

限幅滤波法

优点

缺点

过程简述

算法实现

中位值滤波法

优点

缺点

过程简述

算法实现

算术平均滤波法

优点

缺点

过程简述

算法实现

中位值平均滤波法

优点

缺点

过程简述

算法实现

加权平均值滤波算法

优点

缺点

过程简述

算法实现

递推平均滤波法

优点

缺点

过程简述

算法实现

加权递推平均滤波法

优点

缺点

过程简述

算法实现

低通滤波算法

优点

缺点

过程简述

算法实现

消抖滤波法

优点

缺点

过程简述

算法实现